Tyler Cowen recently linked to a piece by Eric Rasmusen about potential scenarios where immigration hurts the American economy.
Rasmusen considers a few variations on the Cobb-Douglas production function where the amount produced by the economy is given by the equation: $latex Q=L^{.7}K^{.3}$ where L is the total amount of labor and K is the amount of capital available for production.
According to this model, if L = 100 and K = 100, the total production is 100. Of this amount, 70 is divided among the laborers and 30 goes to owners of capital. If L increases to 140 due to immigration and K remains constant, total production increases to 126.6. 38 of this goes to capital, 63.3 goes to native labor and 25.3 goes to immigrant labor. So capital wins and native labor loses. The amount capital gains is a bit more than the amount native labor loses.
This is a pretty standard analysis, but we should note that it assumes that K remains constant. This is the sophisticated equivalent of assuming that the number of jobs is constant, so that when immigrants enter the country they take “our” jobs. In fact, the amount of capital devoted to production depends on demand, which depends on the number of consumers. Since immigrants are consumers in addition to laboersr, we can expect the amount of capital devoted to production to increase.
But this isn’t the biggest complaint I have with the paper. In his analysis of the standard Cobb-Douglas approach, Rasumsen makes some very confusing comments about the impact of taking the welfare of immigrants into consideration:
“What about the benefit to immigrants? Some readers will want to include those in the policy objective for the United States… Although American labor definitely loses, immigrant labor either wins or is unaffected. The aggregate benefit to labor can be negative because if foreign wages are just a little bit lower than American post-immigration wages, then the gain to the immigrant labor is very small, while the loss to American labor is unaffected and therefore exceeds the immigrant gain. In fact, one might expect that if there is open immigration and the amount of immigration is 40, it must be that wages in the other country are .63, i.e., immigration stops at 40 because foreign and American wages equalize. Suppose further that the rest of the world is large compared to America, so that the rise in wages elsewhere in the world as a result of emigration to America is trivial. Then, the immigrants have neither gained nor lost by immigrating to America. The only welfare effects are the loss to American workers and the gain to American capital-owners.”
This analysis is baffling. If we are using the Cobb-Douglas model to understand the impact of immigration on the US, let’s use the same model to understand the global impact. In particular, let’s assume that we have two countries. In the US, L=100 and K=100, so Q=100 just like in Rasmusen’s model. But then let’s assume that there is one other country where labor and capital are out of balance. That is, L = 1000 and K=50 with the result that Q=407.1. Total production between the two countries is 507.1. Now what happens if we open the borders between the two countries? Then we can combine L and K so that L=1100 and K=150. But we don’t simply add the Q’s. In fact, total production is now 605.1. We got an additional 98 production for free!
How did that happen? We even assumed that the US contribution to K didn’t go up in response to the open borders, a likely result that would push the numbers up even more (if K went all the way up too 1100, then production would go up to 1100 as well). The reason is that the best way to maximize output under the Cobb-Douglas model is to evenly distribute the capital among laborers, not to split it up in disproportionate pieces.
Of course, it remains true that if we prevent K from going up then native labor will suffer. In the closed borders regime, the 100 native laborers received a wage of .7 each and the 1000 foreign laborers got .284. Under the open borders regime, all laborers got a wage of .38. Again, this is because we assumed that K remained constant.
Rasmusen includes a few other scenarios in which not only does native labor lose, but net American output per person goes down. The most plausible of these is a scenario in which he assumes that the production function is a modified Cobb-Douglas function $latex Q=(L^{.7}K^{.3})^{.8}$, which represents the idea that we have diminishing returns to the combination of labor and capital. This could be due to a fixed amount of natural resources or land. In the basic model, the amount capital gains is more than the amount native labor loses. With this modified model, the amount capital gains from immigration is less than the amount lost by native labor.
The problem with this model is that it seems to run counter to experience. It would imply that as our population grows, there would be a very strong tendency for GDP per capita to decrease. That is, the result is not specific to immigration. It applies to any form of population increase. Our population has been growing steadily the nation was founded. Here is a graphic showing the results for GDP per capita:
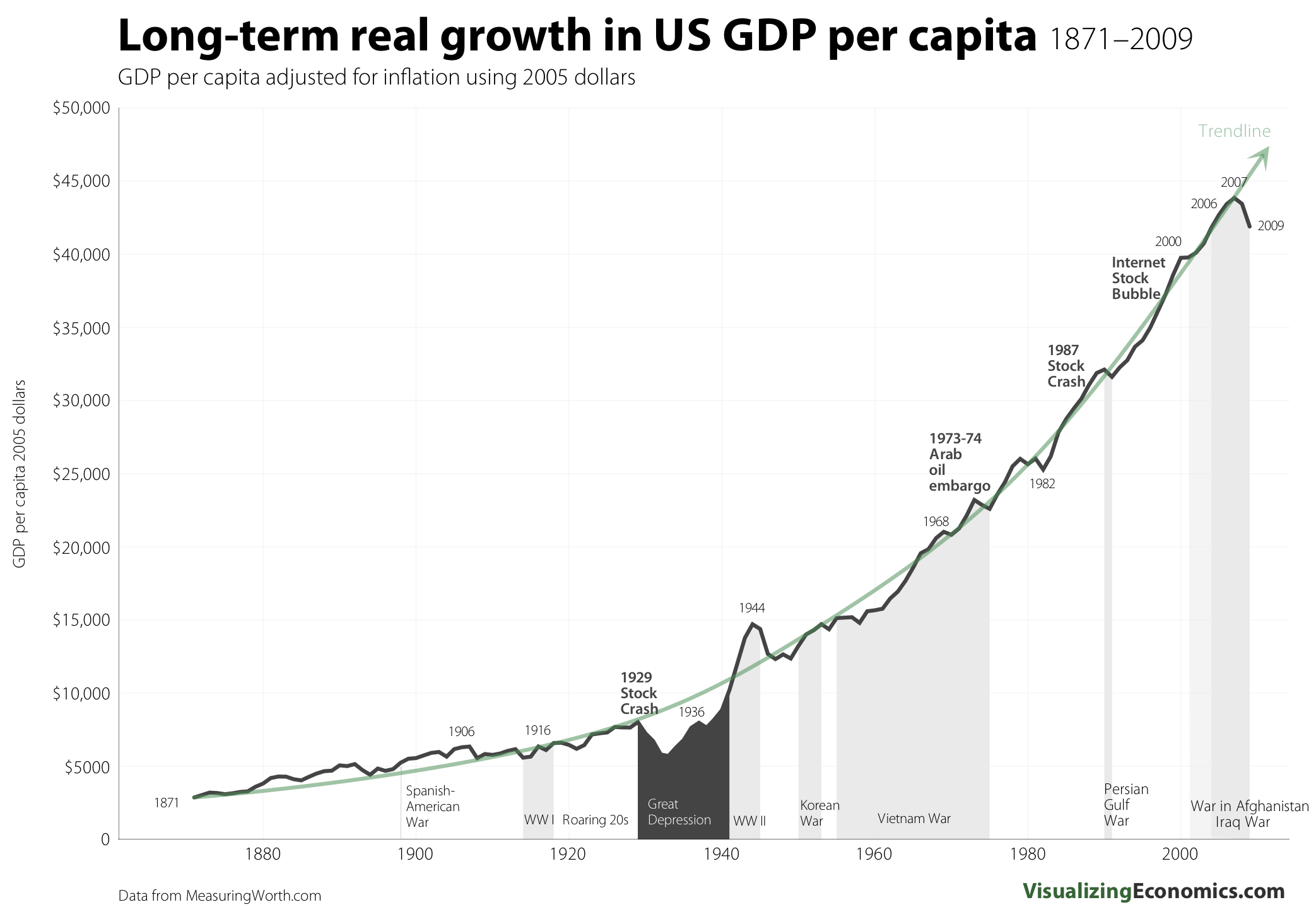
Of course, Rasmusen doesn’t argue that any of his models actually represents reality. He is trying to explore scenarios in which immigration creates a net economic detriment to natives. In the basic model, cash transfers from capital to labor (e.g., progressive taxation) can be used to compensate native labor. In the modified scenario, the net loss to natives prevents such a program from working. Luckily, the model doesn’t seem very realistic, at least based on our historical experience.

“Suppose further that the rest of the world is large compared to America, so that the rise in wages elsewhere in the world as a result of emigration to America is trivial. Then, the immigrants have neither gained nor lost by immigrating to America. The only welfare effects are the loss to American workers and the gain to American capital-owners.”
Here’s Rasmussen’s mistake. If the rest of the world is “large” relative to America– in a pure theory sense this tends to mean “infinitely large”– then even a “trivial” rise in wages for immigrants– in a pure theory sense this means “zero”– multiplied by a “large” world would be significant. Or maybe it’s truer to say that it’s indeterminate in a way that can be presumed in practice to be significant. This is a poor use of economic theory, which confuses rather than elucidates. At any rate, this reasoning isn’t valid or useful in any way.
Let’s see. Suppose ten million workers move from China to America, driving the American wage down to the Chinese wage. Those workers aren’t helped. How about the 1000 million left in China? Yes, I think you’re right— each of them has a slightly higher wage, so they are indeed better off. Thanks for the comment; I’ll change that part. It does seem that the total gain to immigrants and their country has to be positive. I should have seen that.
:”This is a pretty standard analysis, but we should note that it assumes that K remains constant. This is the sophisticated equivalent of assuming that the number of jobs is constant, so that when immigrants enter the country they take “our” jobs. In fact, the amount of capital devoted to production depends on demand, which depends on the number of consumers. Since immigrants are consumers in addition to laboersr, we can expect the amount of capital devoted to production to increase.”
Keeping K the same is reasonable, especially in this context and as a first cut. If immigrants bring their capital ownership with them, that changes the analysis, of course, but in actuality most immigrants own more labor than capital, and we must remember that just because they work in the US does not mean they invest their capital here. In fact, immigrants worldwide are known for sending remittances home, so their investment in domestic capital would be less than that of the natives. A more important objection is that if wages fall in the US then capital will be attracted there— both capital owned by Americans (less foreign investment) and by foreigners. I haven’t analyzed that case. I suspect that with diminishing returns, the result could be that *all* Americans lose from immigration—capital as well as labor— because the immigrant capital drives down the return to capital, and,like the foreign labor, is taking advantage of the US stock of public goods without having ever been taxed for it.
“Now what happens if we open the borders between the two countries? Then we can combine L and K so that L=1100 and K=150. But we don’t simply add the Q’s. In fact, total production is now 605.1. We got an additional 98 production for free!”
Good example. Including the welfare of immigrants will indeed make total welfare rise, in general. My paper was directed at showing the effect on Americans, with only a little discussion of the impact on foreigners.
The Welfare Theorems apply even with diminishing returns. I do have *external* diseconomies of scale here, though, and the Welfare Theorems don’t apply directly. My hunch is that factor price equalization increases total output so long as adding an extra worker does not reduce total output. If adding the extra worker just reduces wages, world surplus rises. If adding the extra worker actually reduces output at some point, then world surplus might fall with immigration.
“The problem with this model is that it seems to run counter to experience. It would imply that as our population grows, there would be a very strong tendency for GDP per capita to decrease.”
That is correct, except it wouldn’t be a strong tendency. And it is true, I think, that if the American population had not increased so fast, per capita income would have been higher. Think about the value of the natural resources alone!
Per capita income has always increased, though, and that is because capital accumulation and, especially, technical change always made up for the increased number of people, so wages kept increasing.
Also, if the population increase takes the form of Americans having children, it’s more reasonable to count the new labor as part of the American objective function; the new people are Americans from birth. It is quite true, though, that the young generation competes in the labor market with the old generation, reducing the wage.
Thanks for joining the conversation. You make a good point that with a smaller population we could have had an even higher gdp/capita. But looking at the data I don’t really see a correlation between population growth and gdp/capita across countries either. Well, there may be a slight negative correlation because Africa has unusually low gdp/capita and high pop growth. But this doesn’t seem like a good way to test the counterfactual of lower population growth.
Also, when you say that it makes more sense to include American children in the American objective function, you implicitly assume that we should have an “American objective function.” From a practical policy perspective this might be a good assumption. But from a moral point of view there is some disagreement about whether we ought to exclude someone from our objective function because they were born outside our borders.
Finally, I agree that assuming K to be constant is okay for a first cut, but the connection between a growing population and K is at the heart of the issue. You are basically making an argument about what happens if we have limited resources, so unless we investigate how K actually changes the results are purely hypothetical.