Monthly Archives: June 2013

Weekly link roundup 1

Leave a comment

This post begins a series of weekly link roundups for links across the web to a diverse range of content. The linked content need not have been published in the past week. As always, linking does not imply endorsement.

Oh, the absurdity of thinking that open borders demands open citizenship

15 Comments

One of the most common misconceptions I encounter in discussing open borders is the casual conflation of open borders with open citizenship. For something I consider an incredibly elementary distinction, this apparently eludes plenty of intelligent people. For example, here is EconLog blogger Art Carden casually saying:

An answer to Bryan’s question about how the government should spend a billion dollars. I’m going to take “give it back to the taxpayers” and “print a few hundred million US passports for prospective immigrants” off the table.

Bryan Caplan is one of the most famous and vocal open borders advocates around; he is Carden’s co-blogger. And yet it apparently seems to have escaped Carden that Caplan has never suggested printing US passports for foreigners. Caplan and the rest of the open borders movement want people to be free to move across borders. And you don’t need a US passport to cross the US border! You just need a valid US visa.

People worried that immigrants are going to abuse their welfare system or cast uninformed votes if we open the borders completely ignore that there are millions of foreigners today who legally cross borders whose access to welfare and the vote are curtailed, if not eliminated, by their visa restrictions. This is true in the US, and it is true in virtually any other country you care to name.

This is why I find the pervasive belief that it’ll be impossible to keep citizenship out of the hands of foreigners so puzzling. Surely people realise that in the US, as in most countries, you don’t need to be a citizen to work or settle now. Why would this change under open borders?

The distinction between open borders and open citizenship is critical. If you assume the first implies the second, you still need to clarify why exactly you believe allowing people to move to your country means you would be forced to give them citizenship. When I raise this distinction, I encounter two types of responses:

  1. A total avoidance of the distinction (i.e. the person persists in assuming you need to be a citizen of a country to live there)
  2. A confident certainty that either:
    1. Immigrants would rise up politically to demand and then acquire citizenship
    2. It would be simply immoral to admit a lot of immigrants and not give them citizenship

For scenario #1, I confess I am lost. It’s possible the fault lies with me in failing to communicate the distinction between passports and visas, between citizen and legal immigrant. But how can we best communicate this distinction? Any ideas?

For the scenarios in #2, let’s use US data, because it’s most conveniently at hand (thank you, my Dartmouth classmate Harry Enten!). In general, only 60% of US legal permanent residents naturalise. For those who were given legal immigrant status by the last major US amnesty, in 1986, only 40% naturalised. In short, almost 1 in 2 legal US immigrants don’t really want citizenship.

And right now, it’s fairly straightforward to acquire US citizenship once you’ve met the simple residency requirement of 5 years; the hardest parts tend to be learning English (if you don’t speak it), learning the material on the citizenship test (a bore, but certainly a doable challenge for most), and putting together the necessary paperwork to show you’re not a criminal, etc. It seems highly questionable to me to claim that these people would have rioted if they’d been admitted legally but under a different, stricter residency requirement.

And on that point, I don’t see any moral reason why the requirement for naturalisation has to be 5 years; it could easily be 15, or even longer. The harm to immigrants from this is minimal. Other than the vote and welfare, most people in the US, lawfully present or not, have identical rights and responsibilities. In fact, the only meaningful harm I can think of is that non-citizens can be deported and citizens can’t be. But the whole point of open borders is that, barring evidence that you are a danger of some kind, you should be able to go where you like. Once we protect non-citizens from arbitrary deportation, the moral harm of raising the bar for citizenship seems almost non-existent. It certainly pales in comparison to the moral harm of keeping people out of your country at gunpoint because you’re afraid letting them in might morally obligate you to throw a blank passport at them.

The question of whether such a moral obligation exists is something worthy of a whole book. But I don’t see a reason why crossing over an arbitrary line should suddenly make people on the other side of that line obligated to give you the vote. Citizenship is fundamentally related to who you are, not where you live, although the two are clearly related. I think most people intuitively understand this, since I don’t see anyone seriously demanding that every person on a student visa or a work permit in a foreign country be permitted to vote there. And I think it shouldn’t be hard to intuitively see that something is wrong with us if we insist on forcefully keeping people jobless and starving because we’re afraid the only alternative is giving them the vote. You don’t need to be a voter to hold down a paying job or rent your own home. So why impose that absurd and arbitrary requirement on someone else?

I am for open borders. I am not for open citizenship. There is a difference, and let’s be clear about that. One is about the fundamental human right to live and work without needing to beg any government for permission to stay in your own home or work for your employer. The other is about the less fundamental political right to cast a vote. The two are not the same, and blurring the difference between them does not serve us well.

Immigration and Cobb-Douglas: A Response to Eric Rasmusen

6 Comments

Tyler Cowen recently linked to a piece by Eric Rasmusen about potential scenarios where immigration hurts the American economy.

Rasmusen considers a few variations on the Cobb-Douglas production function where the amount produced by the economy is given by the equation: $latex Q=L^{.7}K^{.3}$ where L is the total amount of labor and K is the amount of capital available for production.

According to this model, if L = 100 and K = 100, the total production is 100. Of this amount, 70 is divided among the laborers and 30 goes to owners of capital. If L increases to 140 due to immigration and K remains constant, total production increases to 126.6. 38 of this goes to capital, 63.3 goes to native labor and 25.3 goes to immigrant labor. So capital wins and native labor loses. The amount capital gains is a bit more than the amount native labor loses.

This is a pretty standard analysis, but we should note that it assumes that K remains constant. This is the sophisticated equivalent of assuming that the number of jobs is constant, so that when immigrants enter the country they take “our” jobs. In fact, the amount of capital devoted to production depends on demand, which depends on the number of consumers. Since immigrants are consumers in addition to laboersr, we can expect the amount of capital devoted to production to increase.

But this isn’t the biggest complaint I have with the paper. In his analysis of the standard Cobb-Douglas approach, Rasumsen makes some very confusing comments about the impact of taking the welfare of immigrants into consideration:

“What about the benefit to immigrants? Some readers will want to include those in the policy objective for the United States… Although American labor definitely loses, immigrant labor either wins or is unaffected. The aggregate benefit to labor can be negative because if foreign wages are just a little bit lower than American post-immigration wages, then the gain to the immigrant labor is very small, while the loss to American labor is unaffected and therefore exceeds the immigrant gain. In fact, one might expect that if there is open immigration and the amount of immigration is 40, it must be that wages in the other country are .63, i.e., immigration stops at 40 because foreign and American wages equalize. Suppose further that the rest of the world is large compared to America, so that the rise in wages elsewhere in the world as a result of emigration to America is trivial. Then, the immigrants have neither gained nor lost by immigrating to America. The only welfare effects are the loss to American workers and the gain to American capital-owners.”

This analysis is baffling. If we are using the Cobb-Douglas model to understand the impact of immigration on the US, let’s use the same model to understand the global impact. In particular, let’s assume that we have two countries. In the US, L=100 and K=100, so Q=100 just like in Rasmusen’s model. But then let’s assume that there is one other country where labor and capital are out of balance. That is, L = 1000 and K=50 with the result that Q=407.1. Total production between the two countries is 507.1. Now what happens if we open the borders between the two countries? Then we can combine L and K so that L=1100 and K=150. But we don’t simply add the Q’s. In fact, total production is now 605.1. We got an additional 98 production for free!

How did that happen? We even assumed that the US contribution to K didn’t go up in response to the open borders, a likely result that would push the numbers up even more (if K went all the way up too 1100, then production would go up to 1100 as well). The reason is that the best way to maximize output under the Cobb-Douglas model is to evenly distribute the capital among laborers, not to split it up in disproportionate pieces.

Of course, it remains true that if we prevent K from going up then native labor will suffer. In the closed borders regime, the 100 native laborers received a wage of .7 each and the 1000 foreign laborers got .284. Under the open borders regime, all laborers got a wage of .38. Again, this is because we assumed that K remained constant.

Rasmusen includes a few other scenarios in which not only does native labor lose, but net American output per person goes down. The most plausible of these is a scenario in which he assumes that the production function is a modified Cobb-Douglas function $latex Q=(L^{.7}K^{.3})^{.8}$, which represents the idea that we have diminishing returns to the combination of labor and capital. This could be due to a fixed amount of natural resources or land. In the basic model, the amount capital gains is more than the amount native labor loses. With this modified model, the amount capital gains from immigration is less than the amount lost by native labor.

The problem with this model is that it seems to run counter to experience. It would imply that as our population grows, there would be a very strong tendency for GDP per capita to decrease. That is, the result is not specific to immigration. It applies to any form of population increase. Our population has been growing steadily the nation was founded. Here is a graphic showing the results for GDP per capita:

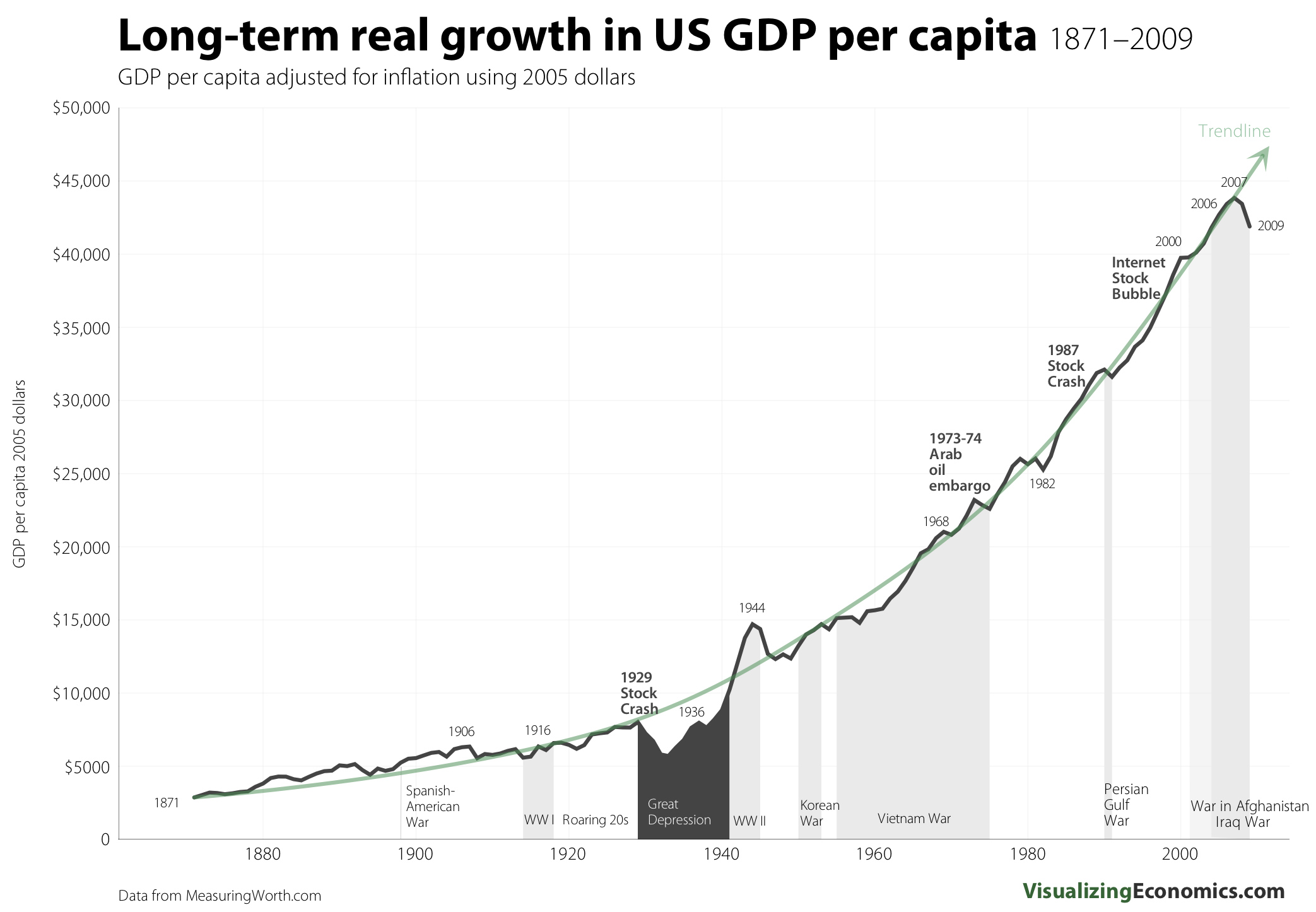
Of course, Rasmusen doesn’t argue that any of his models actually represents reality. He is trying to explore scenarios in which immigration creates a net economic detriment to natives. In the basic model, cash transfers from capital to labor (e.g., progressive taxation) can be used to compensate native labor. In the modified scenario, the net loss to natives prevents such a program from working. Luckily, the model doesn’t seem very realistic, at least based on our historical experience.

 

US visa policy: a cross between Kafka, Orwell, racism, and aristocracy

8 Comments

It’s always fascinating to see an immigration lawyer’s take on how the immigration process works. In 2009, lawyer Angelo Paparelli responded skeptically to then-US Secretary of State Hillary Clinton when she said she would push for a streamlined visa process. Then, he noted the most important thing she could do here would be to pursue the amendment or repeal of an obscure section of the US Immigration and Naturalization Act, noting that this law, § 214(b), is responsible for 99% of all non-immigrant visa refusals:

The 99% rate of § 214(b) refusals is important because:

  • Consular officers are not given sufficient resources to spend more than just a minute or two to consider whether a visa applicant truly deserves to receive a visa.
  • INA § 291 requires a visa refusal if the applicant “fails to establish to the satisfaction of the consular officer that he is eligible to receive a visa.”
  • Under the doctrine of “consular nonreviewability” (which more accurately should be dubbed consular absolutism) as interpreted by the federal courts and the State Department, decisions by consular officers on questions of fact (on which most visa refusals turn) are not reviewable by President Obama, Secretary Clinton or the Supreme Court.

In other words, imagine that you had one or two minutes to establish that you deserve a U.S. nonimmigrant visa. Your burden can only be met if it is “to the satisfaction of the consular officer.” No one but that officer has the power to decide.

Imagine if you had to prove to a government officer in 1 or 2 minutes why you should be allowed to attend university: you have to prove you won’t fail out, you’ll work hard, you won’t drop out (for any reason), and you’ll go far away after you graduate. Or imagine if you wanted to visit a popular tourist destination or travel for work, but had to prove to a government official in 1 or 2 minutes that you would go home afterwards (and wouldn’t abuse your travel approval to, say, move nearby or find a job there). Prove all this, in 1 or 2 minutes. To someone whose decision is final, and can never be overturned.

This particular provision is so noxious that it is cited multiple times in this UC Irvine report on international students in the US. Its repeal or replacement was an explicit recommendation of the report. The American Bar Association has (since 1990, according to Paparelli) recommended that the US government “establish increased due process in consular visa adjudications and a system for administrative review of certain visa denials, including specified principles.”

Yet a 2005 State Department report reviewing section 214(b) suggested the only way to improve it would be to expand it to include all classes of visas other than green cards. The State report explicitly considered the possibility of limiting consular officers’ totalitarian discretion, but rejected this out-of-hand on the basis that any publicly-published standards or requirements for visa approval ran the risk of increasing application fraud. The report stressed instead the importance of officers’ discretion and flexibility in feeling out visa applicants’ intent; no need for any explicit policy here. In other words, the US government doesn’t want you to know how you can get in!

The consequence of consular officers’ power to make or destroy lives in the span of a few minutes? Lord Acton: absolute power corrupts absolutely. Angelo Paparelli later followed up with some of the most ready-at-hand and egregious examples of consular abuse. He brought up two New York Times stories:

  1. Septuagenerian German theatre director Peter Stein being denied a visa because he refused to laugh at a consular officer’s joke and instead complained he had to stand for 2 hours waiting for his consular interview
  2. Former US consular officer Robert Olsen suing State for wrongful termination after he refused to implement a visa policy he considered racist and discriminatory against the poor

The second case is especially striking because Olsen presented documentation for his claims; the full judgment is especially worth reading, and I plan to write about it separately. Just note for now that some documented reasons for denial of US visas which Olsen complained about include gems like “Slimy looking[;] wears jacket on shoulders w/ earring” and “Bad Appearance. Talks POOR.” Paparelli concluded:

Regrettably for most refused visa applicants who lack the notoriety and influence of a Peter Stein, arbitrary consular decisions to deny a visa are virtually impossible to overturn… The Immigration and Nationality Act (INA), as interpreted by the courts, has enshrined in law “doctrines” of “consular nonreviewability” and “consular secrecy” (INA § 222(f) [8 U.S.C. § 1202(f)]) that in virtually all instances deprive the public, the courts and stakeholders (foreign visa applicants and their American sponsors) of a means to hold consular officers accountable. The interests of fair process, impartial consideration, respectful treatment, government transparency, the cultivation of a favorable opinion of the U.S. among citizens of other countries, and the application of solely lawful grounds to grant or deny a visa — all of these are thrown under the bus.

People in the US complain about feeling degraded when they have to choose between an X-ray and a pat down by Transportation Security Administration officials. How about placing your life in the hands of a government official who has the power to cut you off from your education (and, if the State Department had its way with H visas, your job) for something like “Bad Appearance. Talks POOR”? And no government official, not even the President himself, can do anything about it. US citizens may be tempted to complain that their treatment at the hands of the TSA makes them feel like they live in a police state. But it really is the over 1 million people who are refused US visas every year that truly know the feeling of a US government boot stamping on the human face forever. US visa policy:

  1. By design has no clear rules or guidelines
  2. Gives consular officers totalitarian power which not even the President can cross, thus empowering them to oppress people who:
    1. Come from the wrong racial or national background
    2. Look poor

Disdain for basic fairness and human dignity: that’s just plain US visa policy. Have a nice day folks.

The photograph featured at the top of this post is the identification photo of Wong Kim Ark, a descendant of Chinese immigrants to the US who successfully sued the US government for US citizenship in 1898.

The Tanton memo and restrictionism among US Republicans

4 Comments

A few months ago, I blegged for readers’ views on the relation between immigration and US politics. Here’s what I wrote:

Logically, I can make out four broad positions one can stake on immigration and US politics. I’m curious to hear from readers and co-bloggers about the relative merits of the positions:

  1. Immigration good for Democrats, bad for Republicans regardless of either party’s position on immigration. In other words, even if the Republicans took a pro-immigration stance, more immigration would still hurt them. The electing a new people argument offered by Peter Brimelow of VDARE has this structure. Mark Krikorian of CIS also makes similar arguments. This argument naturally appeals to:
    • Those trying to sell restrictionism to the Republican Party.
    • Those trying to sell pro-immigration policies to the Democratic Party.
  2. Immigration good for Republicans, bad for Democrats regardless of either party’s position on immigration. I don’t know anybody who has taken this position, but I’m adding it for logical completeness. This argument naturally appeals to:
    • Those trying to sell pro-immigration policies to the Republican Party.
    • Those trying to sell restrictionism to the Democratic Party.
  3. Immigration good for whichever party adopts a more pro-immigration stance: In this view, both parties need to compete to be more pro-immigration, and whichever party manages to be more pro-immigration will benefit more from immigration. This seems to be the view of many open borders advocates and other pro-immigration forces, such as my co-blogger Nathan here and here. This argument naturally appeals to pro-immigration forces trying to simultaneously make inroads into both parties, setting up a “race to open borders” between both parties.
  4. Immigration bad for whichever party adopts a more pro-immigration stance: In this view, both parties gain from adopting a more restrictionist stance. Restrictionists who are trying to make a broad-based appeal to both parties would find this argument appealing. In this view, the vote of people with restrictionist sympathies matters a lot more than the votes of potential immigrants and their apologists. Thus, whichever party adopts a more pro-immigration stance will lose a lot more in terms of restrictionist votes, even if they gain a few immigrant votes. Such an argument, if believed, would lead to a “race to closed borders” between both parties. Some restrictionists have made these types of arguments, though they’ve largely focused on (1).

The general consensus in the comments, which saw a fair bit of participation from people who are not Open Borders bloggers and have a somewhat critical/skeptical take on open borders, was in favor of point (1). Namely, immigration is good for Democrats and bad for Republicans, and this holds mostly regardless of the parties’ respective stances on immigration. In other words, if the Republicans adopt a more pro-immigration stance, they will see some gains among immigrants, but still won’t get a majority of the immigrant vote, and the overall increase in immigrant numbers would swamp the slight increase in immigrant share (basically, a small increase in the share within the immigrant vote could be overridden by a greater increase in the immigrant vote share relative to the total vote — this is the electing a new people argument).

Nathan in particular dissented from this view. He suggested that there may be more of a case for (3) in the somewhat longer run, i.e., either party could gain from immigrant votes by marketing itself well. This would of course be ideal from the open borders perspective, as I noted above. In this post, I discuss a memo sent out by John Tanton and the extent to which it sheds light on the discussion above.

The Tanton Memo

The Cafe Con Leche Republicans website’s self-description reads: “We are Republicans who think the GOP should be more welcoming to immigrants.” The site recently published a memo by John Tanton (here’s the PDF of the memo) from 2001. For those unfamiliar with John Tanton, he is an anti-immigration activist who played an important role in helping found leading US restrictionist groups such as CIS, FAIR, and NumbersUSA. Many people on the pro-immigration side view Tanton as a mastermind responsible for much of the success of restrictionism in the United States. I suspect that people have a tendency to overplay Tanton’s role (just as critics of libertarianism overplay the influence of the Koch brothers) but his contribution to the human condition (positive or negative, depending on your perspective) is far more than that of most people. I quote the memo in full below (emphasis mine):

Roy Beck [referencing Roy Beck, CEO of NumbersUSA] and I think we have come up with an idea that can actually move the battle lines on the immigration question in our favor. While we are working on other ideas to move Democrats, this one involves using the recently released census data to show Republican members of Congress, the Administration, and the party’s leadership how massive immigration imperils their political future. The goal is to change Republicans’ perception of immigration so that when they encounter the word “immigrant,” their reaction is “Democrat.”

Here’s what the Census Bureau tells us: There are 28.4 million foreign-born persons living in the U.S. (This was before the Census Bureau recently added another 5 millionto their totals, probably mostly more illegals.) The Center for Immigration Studies breaks the numbers down this way. Of the 28.4 million, 5.5 million are illegals, and 500,000 are here on temporary visas, like the HI-9. Of the 22.4 remaining, 10.6 are already citizens. That leaves approximately 12 million legal non-citizens, about 8 million of whom, having lived here the required five years, could be naturalized. The other 4 million are still in the waiting period. And, of course, we’re adding about 1 million or more to the queue each year.

We know about the heavy tilt of recent immigrants toward the Democratic Party, both from polling booth exit surveys, and from regular surveys like the Harris Poll, enclosed as Item 1. These folks vote at least 2 to 1 for Democrats, and even up to 9 to 1 – see The Boston Globe article (Item 2). Mr. Bush got 35% of the Hispanic vote overall; i.e., Mr. Gore got about 65% – a landslide. I could send many similar articles, but will stop with a U.S. News & World Report (Item 3) confirming the saliency of this view.

Our plan is to hire a lobbyist who will carry the following message to Republicans on Capitol Hill and to business leaders: Continued massive immigration will soon cost you political control of the White House and Congress, given the current, even division of the electorate, and the massive infusion of voters about to be made to the Democratic side. We are about to replay the Democratic hegemony of 1933-53, fueled back then by the massive immigration of 1890-1924.

We have a candidate for the lobbying work in James Edwards, a former staffer for a member of the House Immigration Subcommittee, recently a lobbyist with a trade association, and the co-author of The Congressional Politics of Immigration Reform. He has just joined an independent lobbying firm. He’s solidly in our camp, is very well connected in Republican circles, and is willing and able to take on this assignment. We would like to hire him half-time for a year to give this a try. Our budget for this project is $1 00,000. Mr. Edwards would pay his expenses out of his hourly fee of $1 00.00.

May we have your frank opinion of this idea? If you think it plausible, would you be willing to help support it financially?

Implications of the memo

The memo, if legitimate, suggests that Tanton sought funding to promote the position which I label as (1) in my list: immigration good for Democrats, bad for Republicans. The points I make below assume the authenticity of the memo.

  • This memo certainly indicates a definitive strategy on the part of John Tanton and others in restrictionist circles to appeal to Republicans’ political concerns.
  • Tanton wasn’t the first restrictionist to make this sort of argument. Peter Brimelow, founder of VDARE, in which Tanton hasn’t played an important founding or ongoing role, made the electing a new people argument in the pages of National Review back in 1997 (four years before the Tanton memo).
  • Judging by the mostly consistent stance that restrictionist groups have taken in support of this position over the last few years, this strategy seems to have been selected for, though Tanton’s role as an individual in selecting this strategy for all restrictionist groups is questionable.
  • Of course, just because restrictionists chose to focus their resources on the argument doesn’t mean that it is false (unlike what Cafe Con Leche Republicans seems to suggest). In contrast, the reason they selected that argument is possibly because of its element of plausibility and truth. The ideal position from the restrictionist perspective, after all, isn’t (1) but position (4) on my list: Immigration bad for whichever party adopts a more pro-immigration stance. That Tanton and other restrictionists chose to adopt (1) instead of (4) reveals that they were constrained in their narrative by the facts. More in the next point.
  • This and related evidence make it reasonably clear that restrictionists are restrictionists first and foremost, and their political party loyalties, if any, are secondary. Their choice to align with the Republican Party is a strategic choice based on a belief that they can convince the Republican Party more easily about the synergy between restrictionism and the Republican Party, not out of a principled loyalty to the Republican Party. Specific restrictionists may well be Republicans, but others may well feel more at home with the Democratic Party. Even in the memo, Tanton says in the very first para that he will be searching for parallel strategies to woo Democrats. For this reason, Republicans would be well advised, from the perspective of electoral success, to view restrictionists with a good deal of skepticism when restrictionists claim to have Republicans’ best interests at heart. It may so happen that on a particular issue, the restrictionist position coincides with what is electorally favorable to Republicans. But restrictionists have an incentive to exaggerate their case.
  • I don’t think that restrictionists are overall wrong in terms of their very basic numbers (I’m excluding restrictionists such as Ann Coulter for the purpose of this statement). Where I think Republicans may go wrong (from their own electoral success perspective) is in taking restrictionists sufficiently seriously that they don’t consider the possible gains from new, somewhat untested, pro-immigration configurations.

My co-blogger John Lee has argued (here and here) that Republicans may well benefit electorally from smartly chosen pro-migration and pro-migrant strategies, though he is fairly qualified and cautious in selling his case (for instance, John rejects the view that immigrants are likely to become majority Republican, at least in the near future). While I think John makes a fairly good case, a Republican strategist whose job is to provide Republican candidates advice to win elections would surely be advised to account for the possibility of bias in John’ assessment. Insofar as the discussion above suggests that the “immigration good for Democrats, bad for Republicans” meme was deliberately selected and exaggerated by people who are restrictionists first and Republicans second (if at all), similar caution is advised for Republican strategists listening to restrictionists.