Tag Archives: population momentum

Swamping by Immigrants is Hardly Possible

December 6, 2015 Hansjörg Walther 15 Comments

Restrictionists often bring up a scenario where there are so many immigrants that natives become a tiny minority. In this post, I would like to show that under broad conditions this is not possible: immigrants will almost always remain a minority and will not even come close to becoming a majority. Even if they become a majority, it will not last long and that’s only if you make rather extreme assumptions. Actual swamping with a huge majority of immigrants presupposes even more outlandish assumptions. It is not impossible, but more of a theoretical possibility. If you are afraid of such a scenario you can avoid it with a rather modest restriction on the number of immigrants that for most purposes is not too far from open borders.

In the following discussion, I understand the terms “immigrant” and “native” rather literally: an immigrant is someone who immigrates to a country from another country where he grew up (and so he is an adult or at most an adolescent), and a native is someone who grew up in the country or will grow up there. Even more literally, you could understand this as the distinction between those who are foreign-born and those who are native-born. However, this is a rather technical definition. E.g. the current CEO of Daimler, Dieter Zetsche, was born in Istanbul, so you would have to classify him as an immigrant from Turkey in this sense although he has lived in Germany since he was three years old. Whether you view someone as an immigrant or a native should probably depend more on where someone grew up most of the time. Therefore, I will classify also those as natives who come to the country at a very young age even if they were born abroad. If you have ever seen how fast young children can pick up a new language, this is perhaps not unreasonable. Even if you disagree with me and go for the narrower definition, the results do not change a lot.

You could also have a different view because you think that children of immigrants and maybe even their grandchildren and so forth stay close to the culture their ancestors came from. You might assume persistence for some or all of their traits and that also the descendents of immigrants remain foreign (at least for some time and to a certain extent). I will address the implications of such a broader definition below. But for the moment I would like to stick with the narrower definition and define anyone as native who has lived in the country from age 10 on, and all others I will classify as immigrants.

Why is swamping such a convincing scenario for many people? My guess is that they run a naïve analysis as follows: Suppose you have 100 million people in a country, and each year 5 million immigrate. In the following, I assume no population growth for natives and immigrants to make things more transparent. Then after twenty years, there are 100 million immigrants. It would seem that the total population has risen to 200 million, of whom now natives are only 50%. One year down the road, natives apparently become a minority. After a century, you might think there will be a total of 500 million immigrants, so natives make up only one sixth of the total population then. This would be a situation that people probably have in mind, when they speak of the threat of swamping by immigrants.

The problem with this reasoning is that it is false. This is so because the naïve analysis ignores two separate effects.

The first effect is that although each year another 5 million immigrate, the total number of immigrants in the country will not rise indefinitely as a naïve analysis might suggest. If immigrants come at age 25 and have a life expectancy of 80 years, then after 55 years the initial immigrants will have died out on average. Surely, there will be new immigrants, but after a little more than half a century, they only replace immigrants who came earlier. Hence, with a fixed number of immigrants per year, the total number of immigrants in the country will eventually level off. It is a mistake to extrapolate from the growth you see in the beginning to indefinite growth. Here is what it looks like (I use the stylized assumptions from my previous post “Misinterpreting Growth of Immigrant Populations” for mortality, and I assume that immigrants come at age 25):

The immigrant population grows linearly at first. But after about half a century, its growth slows down because previous immigrants die. After about 70 years, growth comes to a standstill, and the immigrant population stabilizes at about 288 million people (the exact number depends on my assumptions, my purpose here is only to demonstrate the effect, not its exact size in all situations).

The first effect is perhaps rather obvious once you have understood it, and it could easily be incorporated into the naïve analysis. So it would still seem as if natives end up in a minority of 1 to 2.88 or slightly more than a quarter of the total population. However, there is another effect that is even stronger and which starts to operate almost right away. And it is far less obvious. This second effect is the momentum effect that I have described in my previous post “Misinterpreting Growth of Immigrant Populations.” Feel free to read the post for further details. I will explain the effect anyway in a few words, so you can get the thrust of it even without this background.

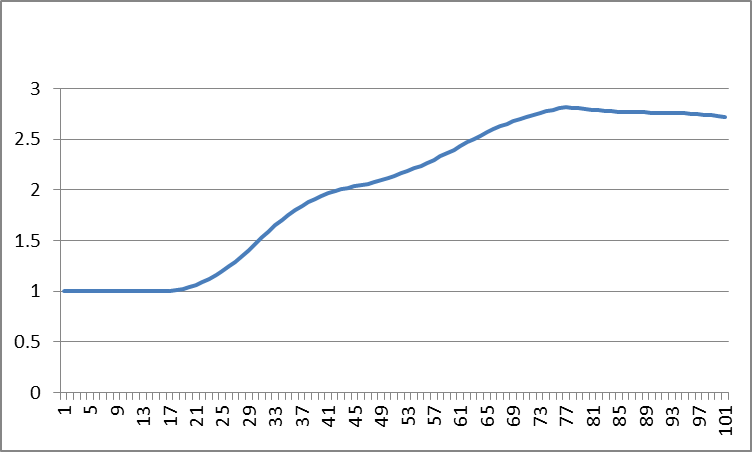
The momentum effect in the above scenario works like this. The 5 million who arrive in one year are mostly young people who will soon start a family. With replacement fertility (my assumption to focus solely on the momentum effect to the exclusion of other effects), they will have about one child per immigrant (two per couple) over the next years. This means there are not only the 5 million immigrants, but also an additional 5 million children who are, by my narrow definition, natives (some of them were technically born abroad, but entered the country at age less than 10). When the children are old enough they again have children. With replacement fertility, those are another 5 million people who are also natives. Hence you have 2 to 1 natives per immigrant. Since a few of the initial immigrants have died by then, the ratio is a little lower (1.76 to 1 with the stylized assumptions in my previous post). Here is what it looks like (note that in my previous post I looked at immigration in one year whereas here I have a fixed number of immigrants each year, so this is an overlay of many such one-time cases):

On the bottom you have immigrants (blue) as in the above graph (by assumption they come at age 25). The next two layers are their children (red), and their grandchildren (green). And the uppermost layer are all their further descendents (i.e. fourth and higher generations). As you can see, the first effect also applies to the second and third generations and for the same reasons, it only comes later. This becomes more obvious over 200 years:

The uppermost layer keeps growing because there is a constant influx of immigrants. Each annual cohort grows into a population 2.76 times as large and then levels off. This means no people are lost, and because there are new immigrants each year, total population keeps growing (eventually by 2.76 times annual immigration per year).

Now, by assumption, there was also an initial native population of 100 million. I will add them to the uppermost layer (basically, this is the assumption that fourth and higher generation immigrants are natives in any sense). Here’s what you get:

Per my narrow definition only the lowest layer consists of immigrants, all the other people are natives. Here is how the share of immigrants in the total population develops over time:

At first, with more and more immigration, the share of immigrants rises. But after some time, their descendents start to expand the native population, so there is a deceleration until the immigrant share peaks slightly below 40%. Later, when the immigrant population stagnates and the population of their descendents keeps growing (plus the initial native population), the share of immigrants falls off again.

Now immigration of 5% of the initial population is very heavy. Why? As you can see in the above graph, total population grows to more than 12 times its initial size over a century. For a country like the US (circa 320 million in 2015), this would mean that population grows to about 4 billion over a century. Possible, but rather extreme as an assumption.

You might object that for smaller countries it could happen. It surely becomes easier. But take a country like Germany with currently some 81 million inhabitants. Its population would rise to one billion people with this level of immigration. But then population density might work as a limiting factor. Population in Germany is now at 226 per square kilometer (583 per square mile). If it went up by a factor of more than 12, then Germany would have an average population density as the most populated parts of Germany have right now. Or in other words: Germany would become one huge city. Possible, but again pretty extreme. And even then the share of immigrants in the total population would not exceed 40% ever. After a century it would even have fallen to below a quarter of total population. Compare this to the result from the naïve analysis how natives will be only one sixth of total population after a century.

Let’s see how the maximum share of immigrants comes out for other levels of annual immigration, and how far one has to go out to achieve a maximum of 50% at least at the peak. Here’s a graph with the number of immigrants per year in millions on the x-axis (reference population of 100 million), and the maximum share of immigrants on the y-axis:

Hence to reach a share of 50% immigrants in the total population (even if only for a short peak after which it falls off again), one would have to have 18 million immigrants each year for an initial population of 100 million. But that implies that total population (even with replacement fertility) will grow to about 45 times its initial size over a century. For the US, this would work out to a population of about 14 billion people, more than total world population according to most projections. And for Germany, it would amount to a population of more than 3.5 billion people. That’s not impossible, but looks rather outlandish as a scenario.

The conclusion from all this is: For all practical purposes, there will never be a majority of immigrants. (I will discuss a few exceptional cases in the appendix, but those do not apply for large countries like the US or Germany. Or you have to make assumptions that would be much worse than swamping .)

Even if you are scared that immigration could become so strong that for a short time immigrants become a majority, all you have to do is introduce a limit on immigration of less than 18 million for an initial population of 100 million. 50 million per year would do for the US, and 14 million for Germany which is orders of magnitude above current levels (below one percent of the population, maybe this year slightly above for Germany).

Now, one objection could be that my definition of immigrants is too narrow, that also second generation immigrants or maybe even third generation immigrants would have to count as immigrants because they stay (partly) foreign. Here is the peak for the share of immigrants, of immigrants + second generation, and of immigrants + second generation + third generation, depending on the number of immigrants per year in millions (reference population 100 million):

The blue line is the line I had above for immigrants alone. The red line is for the first two generations together, and the green line for the first three generations together (the peak occurs at a later point in time, so you do not have these shares at the same time). As for the first two generations: they become a majority for about 1.25 million immigrants per year (initial population of 100 million). As for the first three generations, they become a majority for annual immigration of slightly more than 0.6 million immigrants per year.

Of course, it becomes easier and easier to achieve a majority, the more inclusive the definition of “immigrants” becomes. However, it would still only mean a majority at the peak before it falls off again. While a majority for immigrants is almost impossible, it is conceivable for immigrants + second generation, and even more so, if you add the third generation in. Restrictionists are concerned that a majority could change the culture materially or take the country over via the political process. This may sound more plausible if you assume a vast majority of immigrants who are perhaps rather foreign (but also that they are homogeneous or can easily overcome coordination problems). However, that is hardly possible if you have to include the second or even the third generation. It could only happen if you assume very slow assimilation. I will not pursue this here, but will address this point in a further post.

I only discussed the lowest level of “swamping” so far, i.e. that there is a majority of immigrants at some point in time. To get real “swamping”, one would have to have a much higher share of immigrants. If swamping is something like a level of 80%, it is not possible for immigrants alone, or only under totally outlandish assumptions. It is still hard to achieve for the first two generations together because one would have to go to a level of at least 8.5 million immigrants per year (100 million reference population). And even for the first three generations together, one would have to assume 3.5 million immigrants each year for an initial population of 100 million.

As I already noted above: 5 million immigrants each year is a pretty extreme assumption, and even 3.5 million would still mean that total population grows to more than 9.5 times its initial size over a century. For the US, this would amount to more than three billion people. However, here is what the population structure at the peak after 65 years would look like: 31% immigrants, 33% second generation, 17% third generation, and 19% fourth and higher generations plus initial natives and their descendents. Even with moderate assimilation (e.g. a quarter per generation), the effective share of natives (natives in a narrow sense plus the assimilated part of the first three generations) would be a clear majority even in this scenario. As I said, I will leave a more thorough discussion to a further post. But maybe my conclusion is already clear: only with very low assimilation or even reverse assimilation (i.e. of natives to the immigrant culture) can such a swamping scenario play out with very high immigration. Cultural and political results would also presuppose that immigrants are very homogeneous or at least easy to coordinate.

Let me just sum up the main results of this post:

Under broad assumptions, serious swamping by immigrants is practically impossible. A slight majority at the peak presupposes very high levels of immigration and is also hardly possible. For the first two generations to achieve a majority, you still need rather extreme levels of immigration. Maybe you could see a majority for the first three generations together, but then you also have to make an assumption of very slow assimilation and rather homogeneous immigrants to find this concerning. Even moderate assimilation over three generations would mean that the effectively native part of the population remains a clear majority.

—

Appendix

As I noted above, there are some exceptional cases where something like “swamping” can come to pass. I would like to address them here and also why they are irrelevant for large countries like the US or Germany.

You can have swamping for new settlers on uninhabitated land: there are simply no natives, so the settler culture will prevail by default. This can happen especially in agricultural societies with little need to cooperate with other settlers of a different origin. But then, such a case does not apply for the US or Germany now.
A similar case would be after ethnic cleansing: In a first step you drive away the previous population or kill them off, and then you resettle the new land. You can make such an assumption, but then you should be less concerned about swamping and more about ethnic cleansing and even genocide. And you would have to explain how this is a realistic scenario.
Another variant is if immigration exceeds initial native population by orders of magnitude. E.g. there were a few million Native Americans in what it now the US, and then there was immigration of ten times as many people or so. In addition, there was hardly any incentive or opportunity to assimilate to native culture, so also all descendents remained foreign (as viewed by Native Americans). However, immigration of ten times the current population to the US would mean more than 3 billion immigrants. With the momentum effect, this would build up to an additional population of more than 7 billion. Or in other words: after two generations, everybody in the world would be in the US. Possible, but perhaps a little extreme as an assumption. And then there is no reason to believe there would be no incentive or opportunity to assimilate to American culture. Quite the opposite.
Small countries (more like city states or smaller) can have very high rates of immigration and hence a high share of immigrants, simply because they are so small and it does not take a lot of immigrants. Examples would be American Samoa (40,000 inhabitants and 71% immigrants) or the Carribean Netherlands (12,000 and 66%). However, note: for this to be sustainable you have to have very fast population growth. An example would be New York City where population in 1900 was more than 50 times population in 1800. But again, that cannot happen for large countries or countries which have some constraint for population density.
A funny example, and perhaps the only real example where “swamping” occurs is a country with fertility of 0 and regular immigration. The native population keeps dying out and is being replaced by immigrants. Actually, there is such a country: the Vatican which has 100% immigrants. Strangely enough, no one believes that the culture of the Vatican suffers from this “swamping.”
My argument relies on the momentum effect. If it does not apply or only to a lesser degree then the share of immigrants can become larger. There are several cases where this is possible: (1) The country is a destination for pensioners: they won’t have any children and their previous children might not want to join them. This case is similar to the Vatican. (2) Immigrants who are not allowed to bring in their families. This is the typical situation for the Gulf States where the share of immigrants can be very high: UAE with 84% immigrants, Qatar 74%, and Kuweit 70%. However, this is atypical because it depends on temporary immigration which makes concerns over cultural change or a political takeover a moot point. With permanent immigration the above arguments apply. (3) Immigration of the whole population pyramid including older generations. This can happen with refugees who are forced from their homes. An example of a country with a high share of immigrants because of refugees is Jordan with about 40% immigrants. In this case, there is no or only a mild momentum effect. But note: you also need a rather small country and the share will fall from there because it is hard to sustain the necessary levels of immigration over time. (4) A milder variant of this case is if immigrants come later in life or bring more of their older relatives in (but maybe not all of them). This attentuates the momentum effect and can lead to a higher share of immigrants. However, with a fixed absolute number it also means that effective immigration (people of reproductive age) is lower and the eventual level is lower.
If you exclude all exceptional cases with little import for large countries (thinly populated territories, city states with a hinterland that is not counted, the Gulf States regime) and focus on larger countries, the highest share for immigrants are in Switzerland with 29% immigrants and Australia with 28% immigrants. Although it might seem that those are rather low shares, according to the above analysis, the share of immigrants is already rather high. And a further increase hence presupposes much higher levels of immigration to approach 40% and 50%.
The share of immigrants can be higher with accelerating immigration, e.g. as a fixed percentage of a growing population. However, this means you get exponential growth for the total population instead of linear growth. This makes the situation even less sustainable.
You can have “swamping” by immigrants and all their descendents if there is no assimilation because their numbers keep growing and they remain foreign. With reverse assimilation (to the immigrant culture) the effect could be even stronger. An example would be the Roman Empire where there was a strong incentive for people in newly occupied territories to assimilate to the culture of the Roman “immigrants.” Here immigrants were simply conquerors and it was important for the native population to assimilate to their culture. If you assume that your country is occupied and “immigrants” exert a pull towards their culture because they are in positions of power and wealth, you should be concerned about a military occupation in the first place, not swamping.

—

Miscellaneous Remarks

There seems to be something about Daimler and Turkey. Edzard Reuter, predecessor of Dieter Zetsche, was born in Berlin in 1928. Since his father was a well-known Social Democrat (mayor of Berlin from 1948 to 1953), the family had to flee Germany in 1935 and obtained asylum in Turkey where Edzard Reuter grew up from age 7 to 17. As far as I know he is fluent in Turkish. So you would have to count him as an immigrant from Turkey. Possibly that was his experience in 1945 although he, of course, also had a strong connection with Germany through his family.
If you insist on the share of the foreign-born and not just immigrants who grew up elsewhere, you would have to include the children brought along by immigrants. With my standard assumptions, an immigrant at age 25 brings 0.22 children along. So you would have to increase all numbers by about 22%. But then your assumption is that someone’s birthplace has a deep influence on their development independent of where they grow up or who their parents are. If you think that the environment you grow up in is the most important aspect, then you would end up with my definition (up to small adjustments). And if you think that the important aspect is that parents influence their children, then you would have to look at immigrants and all their children, no matter where they were born. If you think both play a role, you have to take something in between. Classification as “foreign-born” has perhaps more to do with the fact that it is comparably easy to track someone’s birth place versus where they grew up most of the time or what group their parents belong to.
“Swamping” is a vague concept, and it can mean different things to different people. One other sense might be that population in a country rises a lot, and that could have negative consequences. My arguments make such a scenario more probable because they show that immigration leads to more growth than the sheer number of immigrants alone. I can’t have it both ways: If open borders means that many people have a chance to move to rich countries, then the population in rich countries will have to rise. And if a transfer of many people is optimal, then population will have to rise considerably. Assimilation to rather low native fertility in rich countries, mostly below replacement, might mitigate the effect, though, but only over a longer timeframe.
Impeding family reunion works somewhat like the immigration regime in the Gulf States: either children stay in the source country and so immigrants can become a larger share of the total population. Or children immigrate only after they have (partly) grown up in another country and so would have to count as immigrants, too. Keeping children out means that they will not grow up as natives. Since these are the same people, eventually numbers are the same, so such restrictions can only slow the initial build-up down, but do not change the end result. Likewise for bringing in parents and grandparents. They will not change the end result because they will not have an impact on further development.
One assumption that might look like a trick is that I work with replacement fertility. Maybe this is counterintuitive for some, but higher fertility of immigrants makes it even harder for immigrants to become a majority, let alone “swamp” the native population. Since there are now more children and even more grandchildren, immigrants themselves make up a lower share. So if you are concerned about swamping you would have to applaud high fertility. It also tilts the distribution towards those who have been longer in the country and hence are more assimilated.
One other conclusion from the discussion is that every new cohort of immigrants comes to a country that is overwhelmingly native in culture. There is also a strong incentive to assimilate. So there is hardly a chance that native culture will be replaced by some other culture. This is even more so because immigrants are not a homogenous population. Hence it is very plausible that native culture will serve as a lingua franca for various groups of immigrants. This contradicts Nathan Smith’s vision of a country where there are huge masses of people who are not part of native culture (apart from that, I think Nathan Smith also misses the momentum effect and hence his scenario is also implausible in other ways, I will get back to that).

Misinterpreting Growth of Immigrant Populations

November 11, 2015 Hansjörg Walther 16 Comments

I would like to explain an effect that I think is responsible for a lot of misconceptions regarding immigration. If I am right, my explanation shows that some common explanations, while not being entirely false, are mostly irrelevant, or at least of second-order importance. And this also means that conclusions based on such explanations, are off the mark. Explanations that naively extrapolate trends can be especially misleading.

Let me start with an example of what I mean. In 1961, the Federal Republic of Germany and Turkey struck a deal that Turkish “guest workers” (Gastarbeiter) could be hired by German businesses. There were similar treaties also with other countries such as Italy (1955), Greece (1960), or Yugoslavia (1968). 1961 was the year the GDR built the Berlin wall, so rather suddenly the influx of East Germans came to a halt (about 200,000 in 1960). The West German economy was running at full speed with 8.2% annual GDP growth in the 1950s. German businesses were desperately trying to hire additional workers as unemployment fell to below 1%.

So from 1961 to 1971, about 650,000 Turkish guest workers were hired, and until 1976, this grew to about 825,000. What happened in the meantime was that on November 23, 1973, the German government (Social Democrats & Free Democrats) decided to suspend the treaties with Turkey and other countries (except Italy) after a sharp economic downturn and rising unemployment. So no more workers could be hired. In addition, guest workers in Germany were given a choice either to return home or stay permanently. Family reunion was still possible. Only about 135,000 of the 825,000 Turkish guest workers in 1976 were women. Assuming that 135,000 of the male guest workers were married to them and the others would bring in an additional 535,000 women via family reunion, the total would amount to 1.4 million adult immigrants of Turkish descent. Since a return home was encouraged via payments, you would have to subtract a certain number of returnees, though.

And here is what baffles a lot of people: numbers kept going up after 1973. There are now (as per 2013), 2.8 million people of Turkish descent in Germany, roughly a doubling or even more if you assume there was some return migration. Most of the increase came long after 1973, e.g. there were only 2.1 million people with Turkish citizenship in 1998 (that’s when naturalization became rather easy, so up until this point Turkish citizenship usually meant someone was an immigrant or descended from one).

Here are some of the usual suspects to explain the rise: diaspora dynamics, chain migration via family reunion, men marrying women from Turkey and bringing them in, very high birth rates, maybe encouraged by generous welfare benefits, etc. While there is certainly anecdotal evidence for most of this, and also data supporting some of the claims, I think this all is at best a sideshow, and so further conclusions built on such explanations are mostly irrelevant. If I am right, there is nothing baffling about the observation at all, and the explanation is actually rather simple. It is only that a naive analysis tends to overlook the effect I will explain now.

I will work with stylized facts, but the results should not be materially different if you calibrate the model with exact data. Let’s assume that in one year 1 million people immigrate. For the moment let’s also suppose they are 50/50 men and women. To make things more transparent, I assume for the moment that immigrants are 0 years old (of course, that is false, but I will show later how to fix this).

What happens to the initial immigrants over time? Here’s a stylized graph for the percentages over time:

So, no one dies until age 51. Then 1% die per year until age 76 (i.e. a quarter), and 3% per year until age 101 (the rest). This is not entirely true as a certain fraction actually die already before 51, and the real graph is certainly not piecewise linear. However, it is not far off, and life expectation comes out slightly above 80 years which is quite close to reality. I also make the simplifying assumption that men and women have the same mortality. This is not true either, but again not too far off.

How about children? Again I make a simplifying assumption which is roughly in line with reality. The following percentages will have a child at the age on the x-axis (lumping men and women together, so per person, not woman):

The peak is at 30 years, positive rates are from ages 16 to 44. The percentages add up to 100%, i.e. everyone (men and women) has exactly one child or two children per woman. Since no one dies in the relevant age groups (by assumption above), this means you have exactly replacement fertility (that’s why I adjusted reality a little to get confusing effects out of the way). To stress the point: there is no growth that I have built into the model. As you will see, no fancy birth rates are needed.

What happens to the one million initial immigrants in year 0? Since I assumed they are 0 years old, they won’t have any children right away, but starting after 15 years they will. And after some more time, their children will have children, etc. So the immigrant population (including descendents) will develop like this (millions):

Don’t be fooled by the slight downward trend at about 100 years. There is some oscillation, but the number the line converges to is about 2.76. So over time, the one million will grow to 2.76 million. Children and grandchildren come on top. However, initial immigrants eventually die out, so great-grandchildren and further generations only make a minor difference, and the whole population settles into a steady-state. All in all you have almost a tripling, and that’s although I assumed replacement fertility, i.e. no growth at all!

Let’s fix the one unrealistic assumption. Of course, immigrants do not come at age 0. They come perhaps at age 20 (or 30 if you prefer this). But that’s very easy to fix. Just start at 20 (or 30) in the above graph instead of 0. There may be some children that were born before immigration. Add them in under the heading of family reunion which increases the size of initial immigration some. For immigration at age 20, this means that the factor will be slightly less than 2.76. If you take immigration at age 30 instead, then this will boost initial immigration by about 50%, so the factor is somewhat below 2. Note: 2 was about the factor we had for immigrants from Turkey to Germany (2.8 million people of Turkish descent now versus about 1.4 million initial immigrants, but maybe also some return migration). And I did not need any assumptions about massive further family reunion, brides from Turkey, gigantic birth rates, etc.

Here are some conclusions that are easy to read from the graph. Let me assume that immigrants come at age 20 (i.e. the graph starts at year 20). If you like some other age, adapations do not change the conclusions materially which are stylized anyway:

Since there was only immigration in year 0 (i.e. 20 in the above graph), if the government decides to shut down immigration after that, then numbers will keep rising for over 50 years. Restrictionists will be stark staring mad because they are looking for loopholes as an explanation. There should also be calls for even stricter enforcement like a clamp-down on family reunions (although that is not possible by assumption).
Over one generation (by construction on average 30 years), numbers will double. So this seems like a population with an extraordinary growth rate of 2.4% per year (for a doubling). If a population in steady-state (!) were to grow at such rate, it would mean a fertility of 4 per woman (by construction it is exactly 2 per woman). In the first years the increase is even steeper, more like 3% which corresponds to a fertility of about 5 in steady-state. So restrictionists will be looking for the huge families and come up with cultural explanations. And that would even apply here, where it is false by assumption. Higher fertility would not be unimportant, but compared to an additional perceived fertility of 2 or even 3 via the effect it will be second-order for a moderate divergence in fertility.
After one generation, and even two generations, restrictionists may simply extrapolate the trend and conclude how the immigrant population will grow indefinitely and swamp everybody else. However, again by construction, there is no growth, and things will level off eventually. So the extrapolation is totally unwarranted.
After about 50 years, the baffling thing might be that numbers stagnate (as is the case for people of Turkish descent in Germany by now). So there will be amazement over how that could happen.
And one final conclusion that restrictionists usually miss (maybe if they did not, they would have to be very dishonest about the other claims): If you let in one million in the beginning, you will have 2.76 million descendents eventually. Not only the initial immigrants come, but their whole part in the population pyramid at home. (There is a twist that I will explore in a further post: this also means that all those people are missing in the source country.) So if restrictionists understood the effect, they could scale everything up by a factor of 2.76 (or whatever it is exactly calibrating with actual data) and make their stories even scarier.

Just as an extra service, here are the headlines in Germany for the next decades:

2015/2016: There are 1 million Syrian refugees to Germany.
2017: We can’t handle so many people and will close the borders for Syrians. (I am optimistic this will not happen wholesale, but then I want to stay true to the above example.)
2037: How could that happen? We let in just 1 million and clamped down on further immigration, now there are 2 million people here of Syrian descent! Are they smuggling more people in? A reporter has noticed a Syrian family with 10 children. It’s probably their culture. Let’s try to clamp down even more on migration from Syria.
2057: Now there are more than 2.5 million people of Syrian descent. Soon everybody will be Syrian here. What went wrong?
2067: Strange, they always had those extremely large families. Are they now migrating back to Syria?

—

Some further remarks

The basic effect is known as “population momentum,” i.e. population growth has a certain inertia. Even if fertility changes (goes up or down), it takes some time before population growth changes to a new level (higher or lower). You can understand the effect in the following way: if you have a population with no growth, but 1% extra children in one year. Then this is equivalent to 1% immigrants at age zero. So you have the above build-up. There will be another 1% after one generation, and another 1% after two generations (minus some initial “immigrants” who have died in the meantime), and then it levels off.
The effect that I describe is not just population momentum. My main point is about how population momentum is easily misinterpreted in the context of immigration. If you have an extra 1% children in one year, and it builds up to 2.76% extra population over time, anyone who looked at the development would speak of about 1% population growth per generation, which is not very impressive. The reference point here is the whole population. If the extra 1% population are immigrants, however, one may be inclined to take a different reference point: initial immigrants. So the same development would be described as a growth of about 100% per generation, which is much more dramatic. While the two cases are parallel, the perception is quite different.
There is an extra effect that makes the perception even more dramatic. Since immigrants do not immigrate at age 0, but 20, 25, or 30, the first generation appears shortened. It does not take about 30 years for a doubling, but only 5 or 10 years. This adds even more drama. Especially, if someone does a sloppy analysis by comparing data for only two data points (which journalists or the general population are maybe prone to do).

Open Borders: The Case